Analysis and Control of Nonlinear Systems using the LPV Framework

By Patrick Koelewijn May 15, 2023

Introduction

Across various domains in engineering, such as in the mechatronics, the automotive, and the aerospace industry, there is a constant push for higher performance in terms of speed, accuracy, throughput, and power efficiency. These ever-growing performance requirements have led to increasingly complex engineering systems and increasingly complicated models to accurately describe their behavior. The resulting dynamic system models have become dominated by nonlinear, time-varying, or even exhibiting spatially-varying behavior.

While the complexity of dynamic models has increased rapidly over the past decades, most tools commonly used in the industry to analyze and control these systems still rely on results from the Linear Time-Invariant (LTI) framework, which limits the ability to reach the targeted performance requirements. The main advantages of the LTI framework are its systematic, intuitive, computationally efficient and relatively easy-to-use tools for analysis and design of controllers to ensure stability and performance guarantees, which have contributed to its popularity. Moreover, it also provides effective methods to shape the performance of the resulting closed-loop system. Some attempts have been made to extend the systematic LTI results to nonlinear systems through the use of so-called surrogate models. Surrogate modeling approaches, such as the Linear Parameter-Varying (LPV) framework, approximate or embed the nonlinear system dynamics in an easier-to-work-with model structure. This simplifies the analysis and controller design in exchange for some conservativeness in the representation. Although many successful applications of surrogate techniques have led to high industrial interest, naive use of these approaches can lead to improper guarantees of global stability and performance for the underlying nonlinear systems. On the other hand, for nonlinear dynamic systems, there also exist a plethora of results on stability analysis and controller synthesis techniques which operate directly on the nonlinear model. However, for these methods, there is a lack of available approaches for performance shaping. Furthermore, most of the methods are too complex, requiring significant expertise and complicated design choices from the user compared to the easy-to-use methods available for LTI controller design. This heavily hampers the adoption of nonlinear analysis and synthesis techniques in the industry.

A Novel Framework

To this end, we have developed a novel framework for systematic and computationally efficient analysis and control of nonlinear systems to ensure global stability and performance guarantees during my PhD research. In addition, the proposed framework provides intuitive performance shaping, just like in the LTI case. To achieve this, the following crucial questions have been addressed:

  1. How to systematically and computationally efficiently analyze the stability and performance of nonlinear systems?
  2. How to use surrogate representations to achieve convex controller synthesis for nonlinear systems under general performance shaping concepts?
  3. How to reduce the complexity of the used surrogate model for control to ensure computational efficiency for large, complex models?

Global Analysis

To achieve true systematic analysis of nonlinear systems with global stability and performance guarantees, we propose the use of stronger, equilibrium-independent notions, in particular, universal shifted and incremental stability and performance. Using these concepts, stability and performance are analyzed with respect to all (forced) equilibrium points of the system (universal shifted stability) or with respect to convergence to all steady-state trajectories of the system (incremental stability). This makes these notions advantageous to achieve global stability and performance analysis, as they are independent of a particular equilibrium point or trajectory of the system.

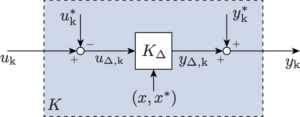
One of our main contributions is to provide a systematic and computationally efficient framework for both universal shifted and incremental stability and performance analysis of Continuous-Time (CT) and Discrete-Time (DT), Multi-Input-Multi-Output (MIMO) nonlinear systems. This is achieved through the development of analysis results for universal shifted and incremental dissipativity analysis with quadratic supply functions. We demonstrate that these analysis conditions can be cast as classical dissipativity tests of linearization-like system representations. Namely, we show how the so-called velocity form of a nonlinear system, representing in CT the time-differentiated dynamics and in DT the time-difference dynamics, can be used to analyze universal shifted stability and performance. For incremental stability and performance analysis, we show how the so-called differential form, which represents the dynamics of the variation around trajectories of the system, can be used. Moreover, we show both the velocity and differential form of the system can be naturally represented through LPV embeddings. This significantly simplifies the analysis problem and, importantly, allows it to be solved computationally efficiently by using various existing LPV techniques.

Figure 1: Chain of implications for system analysis.

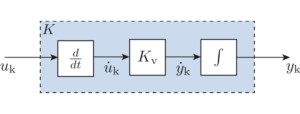
Global Controller Synthesis

Based on the analysis results, we have also developed both universal shifted and incremental controller synthesis algorithms with a crucial nonlinear realization step of the resulting controller for CT and DT, MIMO nonlinear systems. This gives us the universal shifted controller and the incremental controller. Similar to the analysis results, we show that through the LPV framework, a crucial step in the proposed controller design procedures can be cast as a standard LPV synthesis problem. To this end, an intuitive and easy-to-use software implementation to realize the proposed framework-based analysis and controller synthesis has been developed in the LPVcore Toolbox for MATLAB.

Figure 2: Universal shifted controller.
Figure 3: Incremental controller.

Complexity Reduction

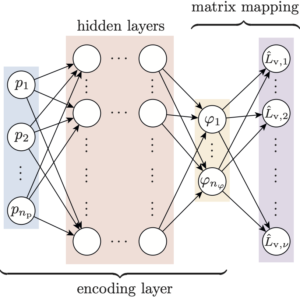
Finally, we have proposed a novel, neural network-based, scheduling dimension reduction method for LPV models. This allows one to reduce the computational burden for the provided LPV-based analysis and controller synthesis results for universal shifted and incremental dissipativity. This is especially of high importance when the developed methods are applied to large-scale, complex systems. Together, these results constitute a systematic and computationally efficient framework for the analysis and control of nonlinear systems with global stability and performance guarantees, while providing intuitive performance shaping.

Figure 4: Neural network architecture for dimension reduction.

Applications

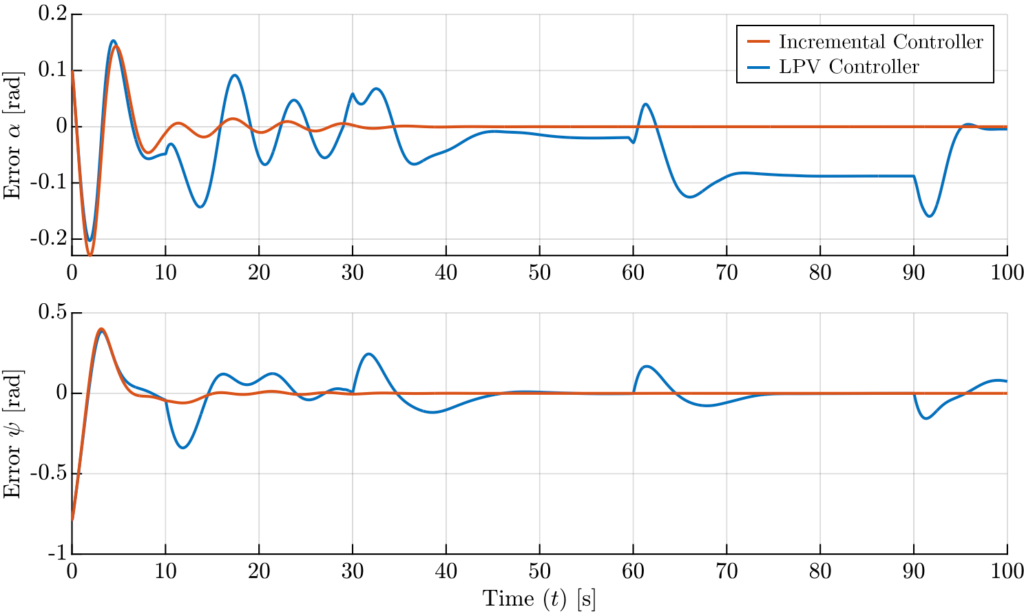
The theoretical results are demonstrated on a wide range of academic examples, lab setups, and real-world applications. For example, we have shown the improved controller performance of our universal shifted controller design for reference tracking and disturbance rejection on a Control Moment Gyroscope (CMG). The incremental controller design is demonstrated when used to design a flight controller for a Generic Parafoil Return Vehicle (GPRV). For both these demonstrations, the benefits of the proposed approaches are shown in terms of improved closed-loop stability and performance properties. Moreover, it is shown that the proposed approaches simultaneously achieve significantly better performance than existing standard LPV control algorithms.

Figure 5: Tracking performance of the universal shifted controller on a CMG, compared to a standard LPV controller.

Figure 6: Tracking error of the incremental controller for flight control of a GPRV, compared to a standard LPV controller.


For more details on this research see:

Koelewijn, P.J.W., ‘Analysis and Control of Nonlinear Systems with Stability and Performance Guarantees: A Linear Parameter-Varying Approach’, PhD Thesis, Electrical Engineering, Eindhoven.